HDU 7110. Shooting Bricks

发表于 分类于

链接

https://acm.hdu.edu.cn/showproblem.php?pid=7110

题意

小红很喜欢玩一个叫打砖块的游戏，这个游戏的规则如下：

在刚开始的时候，有 $n$ 行 $m$ 列的砖块，小红有 $w$ 发子弹。小红每次可以用一发子弹，打碎某一列当前处于这一列最下面的那块砖，并且得到相应的得分。（如图所示）

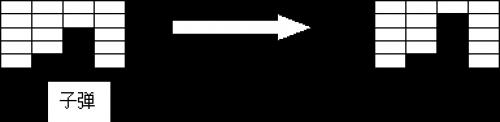
某些砖块在打碎以后，还可能将得到一发子弹的奖励。最后当所有的砖块都打碎了，或者小红没有子弹了，游戏结束。

小红在游戏开始之前，就已经知道每一块砖在打碎以后的得分，并且知道能不能得到一发奖励的子弹。小红想知道在这次游戏中她可能的最大得分，可是这个问题对于她来说太难了，你能帮帮她吗？

N 代表没有奖励，Y 代表有奖励。

$1\le n,m,w \le 200$。

思路

射出子弹可能会返还，那么代表每次射击后子弹数余额要么不变要么减少 $1$ 颗。

容易想到，我们要做的是给每一列确定子弹消耗数。

  • 当某列将分配到的 $x$ 颗子弹全部射完，以 N 结束，那么当前列需要 $x$ 颗子弹；
  • 当某列将分配到的 $x$ 颗子弹全部射完，以 Y 结束，那么当前列需要 $x+1$ 颗子弹，而实际消耗 $x$ 颗。

假设两种情况各有一列，显然我们会先执行后者情况，因为虽然消耗的子弹数一样，但是若后执行后者，那么需要拥有的子弹数会多一颗。

那么对于所有列来说，最终一定会最后射击以 N 结束的某列，除非所有列都是以 Y 结束。

这里的结束指的是将该列分配的子弹消耗完。

记 $sum_{i,j,0}$ 为第 $i$ 列消耗 $j$ 颗子弹以 Y 结束的最大得分，$sum_{i,j,1}$ 为第 $i$ 列消耗 $j$ 颗子弹以 N 结束的最大得分；

$dp_{i,j,0}$ 为前 $i$ 列消耗 $j$ 颗子弹不在 $1\sim i$ 列结束的最大得分，$dp_{i,j,1}$ 为前 $i$ 列消耗 $j$ 颗子弹在 $1\sim i$ 列结束的最大得分：

  1. 最后一列不在前 $i$ 列：

$dp_{i,j,0}=\max\limits_{k\le j}(dp_{i,j,0},dp_{i-1,j-k,0}+sum_{i,k,0})$

因为需要多准备一颗子弹，所以还需满足 $w-j>0$。

  1. 最后一列在第 $i$ 列：

$dp_{i,j,1}=\max\limits_{k\le j}(dp_{i,j,1},dp_{i-1,j-k,0}+sum_{i,k,1})$

此时第 $i$ 列必定消耗子弹，所以还需满足 $k>0$。

  1. 最后一列在前 $i-1$ 列：

$dp_{i,j,1}=\max\limits_{k\le j}(dp_{i,j,1},dp_{i-1,j-k,1}+sum_{i,k,0})$

此时前 $i-1$ 列必定消耗子弹，所以还需满足 $j-k>0$。

将 dp 初始化为 $-inf$，$dp_{0,0,0}$ 初始化为 $0$。

最终取 $dp_{m,1\sim w,0/1}$ 的最大值。

然而存在一个问题，当某列有连续的两个 N 或以 N 结尾时，不存在对应的 $dp_{i,j,0}$。

我们可以将 $dp_{i,j,0}=dp_{i,j,1}$，因为没有后续的 Y，所以不需要多准备一颗子弹，然后仍然可以照上述方程转移。

此时会造成影响的在第一种情况中，即 $j=w$ 时，而 $dp_{i,w,0}$ 并不会转移到后续状态，

若 $dp_{i-1,j-k,0}+sum_{i,k,0}$ 为最大得分，因为 $dp_{i,k,0}=dp_{i,k,1}$，在第二种情况中也会得到更新。

故对最终答案并无影响。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>
#define SZ(x) (int)(x).size()
#define ALL(x) (x).begin(),(x).end()
#define PB push_back
#define EB emplace_back
#define MP make_pair
#define FI first
#define SE second
using namespace std;
typedef double DB;
typedef long double LD;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;
typedef vector<int> VI;
typedef vector<PII> VPII;
// head
const int N=205;
int f[N][N],g[N][N],sum[N][N][2],dp[N][N][2],cnt[N];
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;cin>>T;
    while(T--) {
        int n,m,w;cin>>n>>m>>w;
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=m;j++) {
                char c;
                cin>>f[i][j]>>c;
                g[i][j]=c=='Y';
            }
        }
        for(int j=1;j<=m;j++) {
            cnt[j]=0;
            sum[j][0][0]=sum[j][0][1]=0;
            for(int i=n;i>=1;i--) {
                if(g[i][j]) sum[j][cnt[j]][0]+=f[i][j];
                else {
                    ++cnt[j];
                    sum[j][cnt[j]][0]=sum[j][cnt[j]-1][0]+f[i][j];
                    sum[j][cnt[j]][1]=sum[j][cnt[j]-1][0]+f[i][j];
                }
            }
        }
        memset(dp,0xc0,sizeof dp);
        dp[0][0][0]=0;
        int res=0;
        for(int i=1;i<=m;i++) {
            for(int j=0;j<=w;j++) {
                for(int k=0;k<=cnt[i]&&k<=j;k++) {
                    if(w-j) dp[i][j][0]=max(dp[i][j][0],dp[i-1][j-k][0]+sum[i][k][0]);
                    if(k) dp[i][j][1]=max(dp[i][j][1],dp[i-1][j-k][0]+sum[i][k][1]);
                    if(j-k) dp[i][j][1]=max(dp[i][j][1],dp[i-1][j-k][1]+sum[i][k][0]);
                }
                if(i==m) res=max({res,dp[i][j][0],dp[i][j][1]});
            }
        }
        cout<<res<<'\n';
    }
    return 0;
}